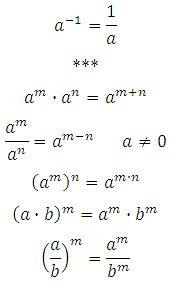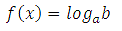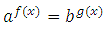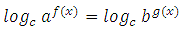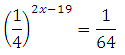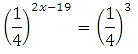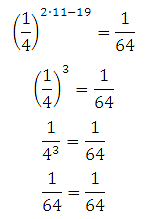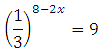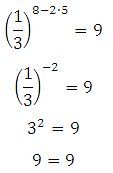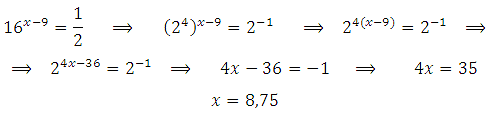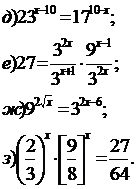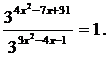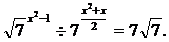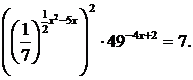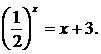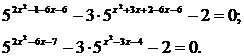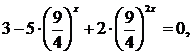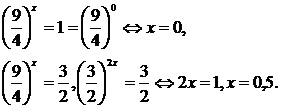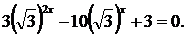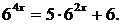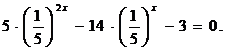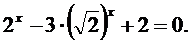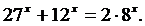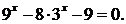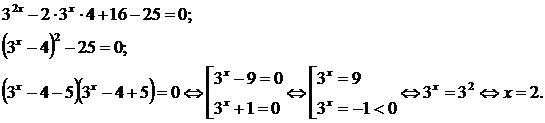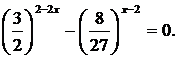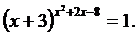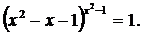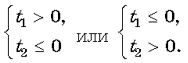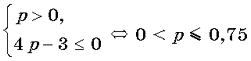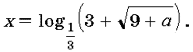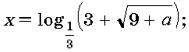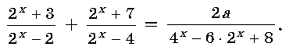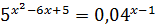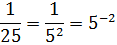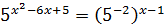На канал на youtube нашого сайту сайт, щоб бути в курсі всіх нових відео уроків.
Для початку згадаємо основні формули ступенів і їх властивості.
Добуток числа a саме на себе відбувається n раз, цей вираз ми можемо записати як a a … A=a n
1. A 0 = 1 (a ≠ 0)
3. A n a m = a n + m
4. (a n) m = a nm
5. A n b n = (ab) n
7. A n / a m = a n — m
Степенні або показові рівняння – це рівняння в яких змінні знаходяться в ступенях (або показниках), а підставою є число.
Приклади показових рівнянь:
У даному прикладі число 6 є підставою воно завжди стоїть внизу, а змінна x ступенем або показником.
Наведемо ще приклади показових рівнянь.
2 x *5=10
16 x — 4 x— 6=0
Тепер розберемо як вирішуються показові рівняння?
Візьмемо просте рівняння:
2 х = 2 3
Такий приклад можна вирішити навіть в розумі. Видно, що x=3. Адже щоб ліва і права частина були рівні потрібно замість x поставити число 3.
А тепер подивимося як потрібно це рішення оформити:
2 х = 2 3
Х = 3
Для того, щоб вирішити таке рівняння, ми прибрали однакові підстави (тобто двійки) і записали те що залишилося, це ступеня. Отримали шукану відповідь.
Тепер підведемо підсумки нашого рішення.
Алгоритм розв’язку показового рівняння:
1. Потрібно перевірити чи однакові підстави у рівняння праворуч і ліворуч. Якщо підстави не однакові шукаємо варіанти для вирішення даного прикладу.
2. Після того як підстави стануть однаковими, прирівнюємо ступеня і вирішуємо отримане нове рівняння.
Тепер прорешаем кілька прикладів:
Почнемо з простого.
Підстави в лівій і правій частині рівні числу 2, значить ми можемо підставу відкинути і прирівняти їх ступеня.
X + 2=4 вийшло найпростіше рівняння.
X=4 — 2
X=2
Відповідь: x=2
У наступному прикладі видно, що підстави різні це 3 і 9.
3 3х-9 х+8 = 0
Для початку переносимо дев’ятку в праву сторону, отримуємо:
Тепер потрібно зробити однакові підстави. Ми знаємо що 9=3 2 . Скористаємося формулою ступенів (a n) m = a nm .
3 3х = (3 2) х+8
Отримаємо 9 х+8 =(3 2) х+8 =3 2х+16
3 3х = 3 2х+16 тепер видно що в лівій і правій стороні підстави однакові і рівні трійці, значить ми їх можемо відкинути і прирівняти ступеня.
3x=2x+16 отримали найпростіше рівняння
3x — 2x=16
X=16
Відповідь: x=16.
Дивимося наступний приклад:
2 2х+4 — 10 4 х = 2 4
В першу чергу дивимося на підстави, підстави різні два і чотири. А нам потрібно, щоб були — однакові. Перетворюємо четвірку за формулою (a n) m = a nm .
4 х = (2 2) х = 2 2х
І ще використовуємо одну формулу a n a m = a n + m:
2 2х+4 = 2 2х 2 4
Додаємо в рівняння:
2 2х 2 4 — 10 2 2х = 24
Ми навели приклад до однакових підстав. Але нам заважають інші числа 10 і 24. Що з ними робити? якщо придивитися видно, що в лівій частині у нас повторюється 2 2х, ось і відповідь-2 2х ми можемо винести за дужки:
2 2х (2 4 — 10) = 24
Порахуємо вираз в дужках:
2 4 — 10 = 16 — 10 = 6
Все рівняння ділимо на 6:
Уявімо 4=2 2:
2 2х = 2 2 підстави однакові, відкидаємо їх і прирівнюємо ступеня.
2х = 2 вийшло найпростіше рівняння. Ділимо його на 2 отримуємо
Х = 1
Відповідь: х = 1.
Вирішимо рівняння:
9 х – 12 * 3 х +27= 0
Перетворимо:
9 х = (3 2) х = 3 2х
Отримуємо рівняння:
3 2х — 12 3 х +27 = 0
Підстави у нас однакові рівні трьом.в даному прикладі видно, що у першої трійки ступінь в два рази (2x) більше, ніж у другої (просто x). В такому випадком можна вирішити методом заміни . Число з найменшим ступенем замінюємо:
Тоді 3 2х = (3 х) 2 = t 2
Замінюємо в рівнянні всі ступені з іксами на t:
T 2 — 12t+27 = 0
Отримуємо квадратне рівняння. Вирішуємо через дискримінант, отримуємо:
D=144-108=36
T 1 = 9
T 2 = 3
Повертаємося до змінної x .
Беремо t 1:
T 1 = 9 = 3 х
Стало бути,
3 х = 9
3 х = 3 2
Х 1 = 2
Один корінь знайшли. Шукаємо другий, з t 2:
T 2 = 3 = 3 х
3 х = 3 1
Х 2 = 1
Відповідь: х 1 = 2; х 2 = 1.
На сайті ви можете в розділі допоможіть вирішити задавати питання ми вам обов’язково відповімо.
Вступайте в групу
Обладнання:
- комп’ютер,
- мультимедійний проектор,
- екран,
- додаток 1 (слайдова презентація в powerpoint) «методи вирішення показових рівнянь»
- додаток 2 (рішення рівняння типу «три різних підстави ступенів» в word)
- додаток 3 (роздатковий матеріал в word для практичної роботи).
- додаток 4 (роздатковий матеріал в word для домашнього завдання).
Хід уроку
1. Організаційний етап
- повідомлення теми уроку (записана на дошці),
- необхідність проведення узагальнюючого уроку в 10-11 класах:
Етап підготовки учнів до активного засвоєння знань
Повторення
Визначення.
Показовим рівнянням називається рівняння, що містить змінну в показнику ступеня (відповідає учень).
Зауваження вчителя. Показові рівняння відносяться до класу трансцендентних рівнянь. Це труднопроизносимое назва говорить про те, що такі рівняння, взагалі кажучи, не вирішуються у вигляді формул.
Їх можна вирішувати тільки наближено чисельними методами на комп’ютерах. А як же бути з екзаменаційними завданнями? вся хитрість полягає в тому, що екзаменатор так складає завдання, що вона якраз допускає аналітичне рішення. Іншими словами, ви можете (і повинні!) виконати такі тотожні перетворення, які зводять дане показове рівняння до найпростішого показового рівняння. Це найпростіше рівняння так і називається: найпростіше показове рівняння. воно вирішується логарифмуванням.
Ситуація з розв’язком показового рівняння нагадує подорож лабіринтом, який спеціально придуманий укладачем задачі. З цих вельми загальних міркувань слідують цілком конкретні рекомендації.
Для успішного вирішення показових рівнянь необхідно:
1. Не тільки активно знати всі показові тотожності, а й знаходити множини значень змінної, на яких ці тотожності визначені, щоб при використанні цих тотожностей не набувати зайвих коренів, а тим більше, – не втрачати розв’язків рівняння.
2. Активно знати всі показові тотожності.
3. Чітко, детально і без помилок проробляти математичні перетворення рівнянь (переносити доданки з однієї частини рівняння в іншу, не забувши про зміну знака, приводити до спільного знаменника дробу тощо). Це називається математичною культурою. При цьому самі викладки повинні робитися автоматично руками, а голова повинна думати про загальну дороговказної нитки рішення. Робити перетворення треба якомога ретельніше і детальніше. Тільки це дасть гарантію вірного безпомилкового рішення. І пам’ятати: невелика арифметична помилка може просто створити трансцендентне рівняння, яке в принципі не вирішується аналітично. Виходить, ви збилися зі шляху і вперлися в стінку лабіринту.
4. Знати методи вирішення завдань (тобто знати всі шляхи проходу по лабіринту рішення). Для правильного орієнтування на кожному етапі вам доведеться (свідомо чи інтуїтивно!):
- визначити тип рівняння;
- згадати відповідний цьому типу метод розв’язання задачі.
Етап узагальнення та систематизації вивченого матеріалу.
Учителем спільно з учнями із залученням комп’ютера проводиться оглядове повторення всіх видів показових рівнянь і методів їх вирішення, складається загальна схема. (використовується навчальна комп’ютерна програма л.я. Боревського «курс математики – 2000», автор презентації в powerpoint – т. Н. Купцова.)
Рис. 1. На малюнку представлена загальна схема всіх типів показових рівнянь.
Як видно з цієї схеми стратегія вирішення показових рівнянь полягає в тому, щоб привести дане показове рівняння до рівняння, перш за все, з однаковими підставами ступенів , а потім – і з однаковими показниками ступенів.
Отримавши рівняння з однаковими підставами і показниками ступенів, ви замінюєте цю ступінь на нову змінну і отримуєте просте алгебраїчне рівняння (зазвичай, дрібно-раціональне або квадратне) щодо цієї нової змінної.
Вирішивши це рівняння і зробивши зворотну заміну, ви в результаті приходите до сукупності найпростіших показових рівнянь, які вирішуються в загальному вигляді за допомогою логарифмування.
Осібно стоять рівняння, в яких зустрічаються лише твори (приватні) ступенів. Скориставшись показовими тотожностями, вдається ці рівняння привести відразу до однієї основи, зокрема – — до найпростішоїПоказовому рівнянню.
Розглянемо, як вирішується показове рівняння з трьома різними підставами ступенів.
(якщо у вчителя є навчальна комп’ютерна програма л.я. Боревського «курс математики – 2000» , то природно працюємо з диском, якщо немає – можна на кожну парту зробити роздруківку такого типу рівняння з неї, представлену нижче.)
Рис. 2. план розв’язання рівняння.
Рис. 3. початок розв’язку рівняння
Рис. 4. закінчення рішення рівняння.
Виконання практичної роботи
Визначити тип рівняння і вирішити його.
1. 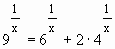
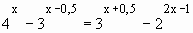
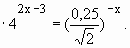
Підведення підсумків уроку
Виставлення оцінок за урок.
Закінчення уроку
Для вчителя
Схема відповідей практичної роботи.
Завдання: із списку рівнянь вибрати рівнянь вказаного типу (№ відповіді занести в таблицю):
- три різні підстави ступенів
- два різних підстави – різні показники ступеня
- підстави ступенів – ступеня одного числа
- однакові підстави – різні показники ступенів
- однакові підстави ступенів – однакові показники ступенів
- твір ступенів
- два різних підстави ступенів – однакові показники
- найпростіші показові рівняння
1.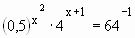
2.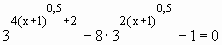
Показові рівняння. Як відомо — до складу єді входять прості рівняння. Деякі ми вже розглянули-це логарифмічні, тригонометричні, раціональні. Тут представлені показові рівняння.
У недавній статті ми попрацювали з показовими виразами, буде корисно. Самі рівняння вирішуються просто і швидко. Потрібно лише знати властивості показників ступеня і… Про це далі.
Перерахуємо властивості показників ступеня:
Нульова ступінь будь-якого числа дорівнює одиниці.
Наслідок з даної властивості:
Ще трохи теорії.
Показовим рівнянням називається рівняння містить змінну в показнику, тобто це рівняння виду:
F (x) вираз, який містить змінну
Методи розв’язання показових рівнянь
1. В результаті перетворень рівняння можна привести до виду:
Тоді застосовуємо властивість:
2. При отриманні рівняння виду a f (x ) = b використовується визначення логарифма, отримаємо:
3. В результаті перетворень можна отримати рівняння виду:
Застосовується логарифмування:
Висловлюємо і знаходимо х.
В задачах варіантів єді досить буде використовувати перший спосіб.
тобто, необхідно представити ліву і праву частини у вигляді ступенів з однаковим підставою, а далі прирівнюємо показники і вирішуємо звичайне лінійне рівняння.
Розглянемо рівняння:
Знайдіть корінь рівняння 4 1–2х = 64.
Необхідно зробити так, щоб в лівій і правій частинах були показові вирази з однією підставою. 64 ми можемо представити як 4 в ступені 3. Отримаємо:
4 1–2х = 4 3
1 – 2х = 3
– 2х = 2
Х = – 1
Перевірка:
4 1-2 (-1) = 64
4 1 + 2 = 64
4 3 = 64
64 = 64
Відповідь: -1
Знайдіть корінь рівняння 3 х–18 = 1/9.
Відомо, що
Означає 3 х-18 = 3 -2
Підстави рівні, можемо прирівняти показники:
Х– 18 = – 2
Х = 16
Перевірка:
3 16-18 = 1/9
3 -2 = 1/9
1/9 = 1/9
Відповідь: 16
Знайдіть корінь рівняння:
Уявімо дріб 1/64 як одну четверту в третьому ступені:
2х – 19 = 3
2х = 22
Х = 11
Перевірка:
Відповідь: 11
Знайдіть корінь рівняння:
Уявімо 1/3 як 3 -1, а 9 як 3 в квадраті, отримаємо:
(3 -1) 8–2х = 3 2
3 -1∙(8–2х) = 3 2
3 -8+2х = 3 2
Тепер можемо прирівняти показники:
– 8+2х = 2
2х = 10
Х = 5
Перевірка:
Відповідь: 5
26654. Знайдіть корінь рівняння:
Рішення:
Відповідь: 8,75
Дійсно, в яку б ступінь ми не звели позитивне число a, ми ніяк не можемо отримати число негативне.
Будь-яке показове рівняння після відповідних перетворень зводиться до вирішення одного або декількох найпростіших. у даній рубриці ми ще розглянемо рішення деяких рівнянь, не пропустіть! на цьому все. Успіху вам!
З повагою, олександр крутицьких.
P. S: буду вдячний вам, якщо розповісте про сайт в соціальних мережах.
Лекція « «методи розв’язання показових рівнянь»»
1 . Показові рівняння.
Рівняння, що містять невідомі в показнику ступеня, називаються показовими рівняннями. Найпростішим з них є рівняння ах = b, де а>0, а ≈ 1.
1) при b< 0 і b = 0 це рівняння, згідно властивості 1 показової функції, не має рішення.
2) при b> 0 використовуючи монотонність функції і теорему про корінь, рівняння має єдиний корінь. Для того, щоб його знайти, треба b представити у вигляді b = ас, ах = bс ó x = c або x = logab.
Показові рівняння шляхом алгебраїчних перетворень призводять до стандартних рівняння, які вирішуються, використовуючи такі методи:
1) метод приведення до однієї основи ;
2) метод оцінки;
3) графічний метод;
4) метод введення нових змінних;
5) метод розкладання на множники;
6) показово-степенні рівняння;
7) показові з параметром.
2 . Метод приведення до однієї основи.
Спосіб заснований на наступному властивості ступенів: якщо рівні два ступені і рівні їх підстави, то рівні і їх показники, тобто рівняння треба спробувати звести до виду
Приклади. розв’язати рівняння:
1 . 3x = 81;
Уявімо праву частину рівняння у вигляді 81 = 34 і запишемо рівняння, рівносильне вихідного 3 x = 34; x = 4. Відповідь: 4.
2. https://pandia.ru/text/80/142/images/image004_8.png «width= «52»height=»49″>і перейдемо до рівняння для показників ступенів 3x+1 = 3 – 5x; 8x = 4; x = 0,5. Відповідь: 0,5.
3. https://pandia.ru/text/80/142/images/image006_8.png»width=» 105″height=»47″>
Зауважимо, що числа 0,2 , 0,04 , √5 і 25 являють собою ступені числа 5. Скористаємося цим і перетворимо вихідне рівняння наступним чином:
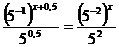
5. 3x = 5. За визначенням логарифма x = log35. Відповідь: log35.
6. 62x+4 = 33x. 2x+8.
Перепишемо рівняння у вигляді 32x+4.22 x+4 = 32x.2x+8, т. Е..png» width=»181″ height=»49 src=»>звідси x-4 =0, x = 4. Відповідь: 4.
7 . 2∙3x+1 — 6∙3x-2 — 3x = 9. Використовуючи властивості ступенів, запишемо рівняння у вигляді 6∙3x – 2∙3x-3x = 9 далі 3∙3x = 9, 3x+1 = 32 , тобто x+1 = 2, x =1. Відповідь: 1.
Банк №1.
Вирішити рівняння:
Тест №1.
1) 0 2) 4 3) -2 4) -4
А2 32x-8 = √3.
1)17/4 2) 17 3) 13/2 4) -17/4
А3
1) 3;1 2) -3;-1 3) 0;2 4) коренів немає
1) 7;1 2) коренів немає 3) -7;1 4) -1;-7
А5
1) 0;2; 2) 0;2;3 3) 0 4) -2;-3;0
А6
1) -1 2) 0 3) 2 4) 1
Тест №2
А1
1) 3 2) -1;3 3) -1;-3 4) 3;-1
А2
1) 14/3 2) -14/3 3) -17 4) 11
А3
1) 2;-1 2) коренів немає 3) 0 4) -2;1
А4
1) -4 2) 2 3) -2 4) -4;2
А5
1) 3 2) -3;1 3) -1 4) -1;3
3 метод оцінки.
Теорема про корінь : якщо функція f (x) зростає(убуває) на проміжку i, число а –будь-яке значення прийняте f на цьому проміжку, тоді рівняння f (x) = а має єдиний корінь на проміжку i.
При вирішенні рівнянь методом оцінки використовується ця теорема і властивості монотонності функції.
Приклади. розв’язати рівняння: 1. 4x = 5 – x.
Рішення. Перепишемо рівняння у вигляді 4x + x = 5.
1. Якщо x = 1, то 41 + 1 = 5 , 5 = 5 вірно, значить 1 – корінь рівняння.
Функція f(x) = 4x – зростає на r, і g(x) = x –зростає на r =>h(x)= f(x)+g(x) зростає на r, як сума зростаючих функцій, значить x = 1 – єдиний корінь рівняння 4x = 5 – x. Відповідь: 1.
2.
Рішення. Перепишемо рівняння у вигляді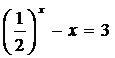
1. Якщо x = -1, то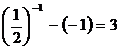
2. Доведемо, що він єдиний.
3. Функція f(x) = — убуває на r, і g(x) = — x – убуває на r=>h(x) = f(x)+g (x) – убуває на r, як сума спадних функцій. Значить за теоремою про корінь, x = -1-єдиний корінь рівняння. Відповідь: -1.
Банк завдань № 2. розв’язати рівняння
А) 4x + 1 =6 – x;
Б)
В) 2x – 2 =1-x;
4. Метод введення нових змінних.
Метод описаний в п.2.1. Введення нової змінної (підстановка) зазвичай проводиться після перетворень (спрощення) членів рівняння. Розглянемо приклади.
Приклади. р еше рівняння: 1. 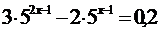
Перепишемо рівняння інакше: https://pandia.ru/text/80/142/images/image030_0.png » width=»128″height=» 48 src= «>тобто..png » width=»210″height=» 45 «>
Рішення. Перепишемо рівняння інакше:
Позначимо https://pandia.ru/text/80/142/images/image035_0.png » width=»245″height=» 57 «>- не підходить.
T = 4 =>https://pandia.ru/text/80/142/images/image037_0.png » width=»268″height=» 51 «>- ірраціональне рівняння. Відзначаємо, що
Рішенням рівняння є x = 2,5 ≤ 4, значить 2,5 – корінь рівняння. Відповідь: 2,5.
Рішення. Перепишемо рівняння у вигляді і розділимо його обидві частини на 56x+6 ≈ 0. Отримаємо рівняння
2×2-6x-7 = 2×2-6x-8 +1 = 2(x2-3x-4)+1, т..png «width=» 118 «height=» 56 «>
Коріння квадратного рівняння – t1 = 1 і t2 .
Рішення. Перепишемо рівняння у вигляді
І зауважимо, що воно є однорідним рівнянням другого ступеня.
Розділимо рівняння на 42x, отримаємо
Замінимо https://pandia.ru/text/80/142/images/image049_0.png » width=»16″height=» 41 src= «>.
Відповідь: 0; 0,5.
Банк завдань № 3. розв’язати рівняння
Б)
Г)
Тест № 3 з вибором відповіді. Мінімальний рівень.
А1
1) -0,2;2 2) log52 3) — log52 4) 2
А2 0,52 x – 3 0,5 x +2 = 0.
1) 2;1 2) -1;0 3) коренів немає 4) 0
1) 0 2) 1; -1/3 3) 1 4) 5
А4 52x — 5x-600 = 0.
1) -24;25 2) -24,5; 25,5 3) 25 4) 2
1) коренів немає 2) 2;4 3) 3 4) -1;2
Тест № 4 з вибором відповіді. Загальний рівень.
А1
1) 2;1 2) ½ ;0 3)2;0 4) 0
А2 2x — (0,5) 2x — (0,5)x + 1 = 0
1) -1;1 2) 0 3) -1;0;1 4) 1
1) 64 2) -14 3) 3 4) 8
1)-1 2) 1 3) -1;1 4) 0
А5
1) 0 2) 1 3) 0;1 4) коренів немає
5. Метод розкладання на множники.
1. Вирішіть рівняння: 5x+1 — 5x-1 = 24.
Рішення..png «width=» 169 «height= «69»>, звідки
2. 6x + 6x+1 = 2x + 2x+1 + 2x+2.
Рішення. Винесемо за дужки в лівій частині рівняння 6x, а в правій частині – 2x. Отримаємо рівняння 6x(1+6) = 2x(1+2+4) ó 6x = 2x.
Так як 2x>0 при всіх x, можна обидві частини цього рівняння поділити на 2x, не побоюючись при цьому втрати рішень. Отримаємо 3x = 1ó x = 0.
3.
Рішення. Вирішимо рівняння методом розкладання на множники.
Виділимо квадрат двучлена
4. Https://pandia.ru/text/80/142/images/image067_0.png «width=» 500 «height=» 181 «>
X = -2 – корінь рівняння.
Рівняння x + 1 = 0 » style=»border-collapse:collapse;border:none»>
А1 5x-1 +5x-5x+1 =-19.
1) 1 2) 95/4 3) 0 4) -1
А2 3x+1 +3x-1 =270.
1) 2 2) -4 3) 0 4) 4
А3 32x+32x + 1 -108 = 0. X=1,5
1) 0,2 2) 1,5 3) -1,5 4) 3
1) 1 2) -3 3) -1 4) 0
А5 2x-2x-4 = 15. X=4
1) -4 2) 4 3) -4;4 4) 2
Тест № 6 загальний рівень.
А1 (22x-1)(24x+22x+1)=7.
1) ½ 2) 2 3) -1;3 4) 0,2
А2
1) 2,5 2) 3;4 3) log43/2 4) 0
А3 2x-1-3x=3x-1-2x+2.
1) 2 2) -1 3) 3 4) -3
А4
1) 1,5 2) 3 3) 1 4) -4
А5
1) 2 2) -2 3) 5 4) 0
6. Показово-степенні рівняння.
До показових рівнянь примикають так звані показово – статечні рівняння, тобто рівняння виду (f(x))g(x) = (f(x))h(x).
Якщо відомо, що f(x)>0 і f(x) ≈ 1, то рівняння, як і показове, вирішується прирівнюванням показників g(x) = f(x).
Якщо умовою не виключається можливість f(x)=0 і f (x)=1, то доводиться розглядати і ці випадки при вирішенні показово – статечного рівняння.
1..png» width=»182″ height=»116 src=»>
2.
Рішення. X2 +2x-8 – має сенс при будь-яких x, т. К. Многочлен, отже рівняння рівносильно сукупності
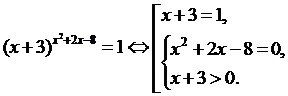
Б)
7. Показові рівняння з параметрами.
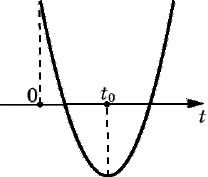
1. При яких значеннях параметра p рівняння 4 (5 – 3) ≈ 2 +4p2–3p = 0 (1) має єдине рішення?
Рішення. Введемо заміну 2x = t, t>0, тоді рівняння (1) набуде вигляду t2 – (5p – 3)t + 4p2 – 3p = 0. (2)
Дискримінант рівняння (2)d = (5p – 3) 2 – 4(4p2 – 3p) = 9 (p – 1) 2.
Рівняння (1) має єдине рішення, якщо рівняння (2) має один позитивний корінь. Це можливо в наступних випадках.
1. Якщо d = 0, тобто p = 1, тоді рівняння (2) набуде вигляду t2 – 2t + 1 = 0, звідси t = 1, отже, рівняння (1) має єдине рішення x = 0.
2. Якщо p1, то 9(p – 1)2>0, тоді рівняння (2) має два різних кореня t1 = p, t2 = 4p – 3. Умові задачі задовольняє сукупність систем
Підставляючи t1 і t2 в системи, маємо
Https://pandia.ru/text/80/142/images/image084_0.png «alt=» no35_11 «width=» 375 » height=»54″> залежно від параметра a?
Рішення. Нехай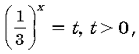
Знайдемо значення параметра a, при яких хоча б один корінь рівняння (4) задовольняє умові t>0.
Введемо функцію f(t) = t2 – 6t – a. Можливі наступні випадки.
Https://pandia.ru/text/80/142/images/image087.png»alt=» http://1september.ru/ru/mat/2002/35/no35_14.gif «align=» left «width=» 215 «height=» 73 src=»>де t0-абсцису вершини параболи і d-дискримінант квадратного тричлена f (t);
Https://pandia.ru/text/80/142/images/image089.png»alt=» http://1september.ru/ru/mat/2002/35/no35_16.gif «align= «left»width=» 60″height=»51 src=»>
Випадок 2. Рівняння (4) має єдине позитивне рішення, якщо
D = 0, якщо a = – 9, тоді рівняння (4)набуде вигляду (t – 3) 2 = 0, t = 3, x = – 1.
Випадок 3. Рівняння (4) має два корені, але один з них не задовольняє нерівності t>0. Це можливо, якщо
Таким чином, при a ≈ 0 рівняння (4) має єдиний позитивний корінь
При a<- 9 рівняння (3) коренів не має.
Якщо a ≈ 0, то Порівняємо способи вирішення рівнянь (1) і (3). Відзначимо, що при вирішенні рівняння (1) було зведено до квадратного рівняння, дискримінант якого — повний квадрат; тим самим коріння рівняння (2) відразу були обчислені за формулою коренів квадратного рівняння, а далі щодо цих коренів були зроблені висновки. Рівняння (3) було зведено до квадратного рівняння (4), дискримінант якого не є повним квадратом, тому при вирішенні рівняння (3) доцільно використовувати теореми про розташування коренів квадратного тричлена і графічну модель. Зауважимо, що рівняння (4) можна вирішити, використовуючи теорему вієта. Вирішимо більш складні рівняння. Завдання 3. Вирішіть рівняння Рішення. Одз: x1, x2. Введемо заміну. Нехай 2x = t, t>0, тоді в результаті перетворень рівняння набуде вигляду t2 + 2t – 13 – a = 0. ( * ) знайдемо значення a, при яких хоча б один корінь рівняння (*) задовольняє умові t>0. Https://pandia.ru/text/80/142/images/image098.png»alt=» http://1september.ru/ru/mat/2002/35/no35_23.gif «align= «left»width=» 71″height=»68 src=»>де t0 — абсциса вершини f(t) = t2 + 2t – 13 – a, d — дискримінант квадратного тричлена f(t). Https://pandia.ru/text/80/142/images/image100.png» alt=»http://1september.ru/ru/mat/2002/35/no35_25.gif» align=»left» width=»360″ height=»32 src=»> Https://pandia.ru/text/80/142/images/image102.png»alt=» http://1september.ru/ru/mat/2002/35/no35_27.gif «align=» left «width=» 218 «height=» 42 src= «> Відповідь: якщо a>- 13, a 11, a 5, то якщо a – 13, A = 11, a = 5, то коренів немає. Список використаної літератури. 1. Гузєєв заснування освітньої технології. 2. Гузєєв технологія: від прийому до філософії. М. «директор школи»№4, 1996 р. 3. Гузєєв та організаційні форми навчання. 4. Гузєєв і практика інтегральної освітньої технології. М. «народна освіта», 2001 р. 5. Гузєєв з форм уроку-семінару. Математика в школі №2, 1987 р.с. 9-11. 6. Селевко освітні технології. М. «народна освіта», 1998 р. 7. Епішева школярів вчитися математиці. М. «просвіта», 1990 р. 8. Іванова підготувати уроки-практикуми. Математика в школі № 6, 1990 р.с. 37-40. 9. Смирнова модель навчання математики. Математика в школі №1, 1997 р.с. 32-36. 10. Тарасенко способи організації практичної роботи . Математика в школі №1, 1993 р.с. 27-28. 11. Про один з видів індивідуальної роботи. Математика в школі №2, 1994 р.с. 63-64. 12. Хазанкін творчі здібності школярів. Математика в школі №2, 1989 р.с. 10. 13. Сканаві. Видавець, 1997 р. 14. Алгебра і початку аналізу. Дидактичні матеріали для 15. Кривоногов завдання з математики. М. «перше вересня», 2002 р. 16. Черкасов. Довідник для старшокласників і Вступників до вузів. «а з т-прес школа», 2002 р. 17. Жевняк для вступників до вузів. Мінськ і рф «обозрение», 1996 р. 18. Письмовий д. Готуємося до іспиту з математики. М. Рольф, 1999 р. 19. Вчимося вирішувати рівняння і нерівності. М. «інтелект-центр», 2003 р. 20. Та ін. Навчально-тренувальні матеріали для підготовки до е г е. М. «інтелект – центр», 2003 р. І 2004 р. 21 та ін. Центр тестування мо рф, 2002 р., 2003р. 22. Гольдберг рівняння. » квант » №3, 1971 р. 23. Волович м. Як успішно навчати математиці. Математика, 1997 р. №3. 24 окунев за урок, діти! м. Просвітництво, 1988 р. 25. Якиманська-орієнтоване навчання в школі. 26. Лійметс робота на уроці. М. Знання, 1975 р. 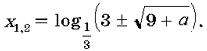
Що таке показове рівняння? приклад.
Отже, показове рівняння … Новий унікальний експонат на нашій загальній виставці найрізноманітніших рівнянь!) як це майже завжди буває, ключовим словом будь-якого нового математичного терміна є відповідний прикметник, який його характеризує. Так і тут. Ключовим словом у терміні «показове рівняння «є слово» показове». Що воно означає? це слово означає, що невідоме (ікс) знаходиться в показниках будь-яких ступенів. і тільки там! це вкрай важливо.
Наприклад, такі прості рівняння:
3 x +1 = 81
5 x + 5 x +2 = 130
4·2 2 x -17 * 2 x +4 = 0
Або навіть такі монстри:
2 sin x = 0,5
Прошу відразу звернути увагу на одну важливу річ: в підставах ступенів (знизу) – тільки числа . А ось в показниках ступенів (зверху) — найрізноманітніші вирази з іксом. Абсолютно будь-які.) все від конкретного рівняння залежить. Якщо, раптом, в рівнянні вилізе ікс де-небудь ще, крім показника (скажімо, 3 x = 18+x 2), то таке рівняння буде вже рівнянням змішаного типу . Такі рівняння не мають чітких правил розв’язку. Тому в даному уроці ми їх розглядати не будемо. На радість учням.) тут ми будемо розглядати тільки показові рівняння в» чистому » вигляді.
Взагалі кажучи, навіть чисті показові рівняння чітко вирішуються далеко не всі і не завжди. Але серед усього багатого різноманіття показових рівнянь є певні типи, які вирішувати можна і потрібно. Ось саме ці типи рівнянь ми з вами і розглянемо. І приклади обов’язково порішаємо.) так що влаштовуємося зручніше і-в дорогу! як і в комп’ютерних «стрілялках», наша подорож буде проходити за рівнями.) від елементарного до простого, від простого – до середнього і від середнього — до складного. По дорозі вас також чекатиме секретний рівень-прийоми і методи вирішення нестандартних прикладів. Ті, про які ви не прочитаєте в більшості шкільних підручників… Ну, а в кінці вас, зрозуміло, чекає фінальний бос у вигляді домашки.)
Рівень 0. Що таке найпростіше показове рівняння? рішення найпростіших показових рівнянь.
Для початку розглянемо якусь відверту елементарщину. З чогось же треба починати, вірно? наприклад, таке рівняння:
2 х = 2 2
Навіть без жодних теорій, за простою логікою і здоровим глуздом ясно, що х = 2. Інакше ж ніяк, вірно? ніяке інше значення ікса не годиться… А тепер звернемо наш погляд на запис рішення цього крутого показового рівняння:
2 х = 2 2
Х = 2
Що ж у нас сталося? а сталося наступне. Ми, фактично, взяли і … Просто викинули однакові підстави (двійки)! зовсім викинули. І, що радує, потрапили в яблучко!
Так, дійсно, якщо в показовому рівнянні зліва і справа стоять однакові числа в яких завгодно ступенях, то ці числа можна відкинути і просто прирівняти показники ступенів. Математика дозволяє.) і далі можна працювати вже окремо з показниками і вирішувати куди більш просте рівняння. Здорово, правда?
Ось і ключова ідея вирішення будь-якого (так-так, саме будь-якого!) показового рівняння: за допомогою тотожних перетворень необхідно домогтися того, щоб зліва і справа в рівнянні стояли однакові числа-підстави в різних ступенях. А далі можна сміливо прибрати однакові підстави і прирівняти показники ступенів. І працювати з більш простим рівнянням.
А тепер запам’ятовуємо залізне правило: прибирати однакові підстави можна тоді і тільки тоді, коли в рівнянні зліва і справа числа-підстави стоять в гордій самоті.
Що значить, в гордій самоті? це означає, без жодних сусідів і коефіцієнтів. Пояснювати.
Наприклад, у рівнянні
3·3 x-5 = 3 2 x +1
Трійки прибирати не можна! чому? тому що зліва у нас стоїть не просто самотня трійка в ступені, а твір 3·3 x-5 . Зайва трійка заважає: коефіцієнт, розумієш.)
Те ж саме можна сказати і про рівняння
5 3 x = 5 2 x +5 x
Тут теж всі підстави однакові – п’ятірка. Але справа у нас не самотня ступінь п’ятірки: там-сума ступенів!
Коротше кажучи, прибирати однакові підстави ми маємо право лише тоді, коли наше показове рівняння виглядає так і тільки так:
a f (x ) = a g (x )
Такий вид показового рівняння називають найпростішим . Або, по-науковому, канонічним . І яке б накручене рівняння перед нами не було, ми його, так чи інакше, будемо зводити саме до такого найпростішого (канонічного) виду. Або, в деяких випадках, до сукупності рівнянь такого виду. Тоді наше найпростіше рівняння можна в загальному вигляді переписати ось так:
F(x) = g(x)
І все. Це буде еквівалентним перетворенням. При цьому в якості f (x) і g(x) можуть стояти абсолютно будь-які вирази з іксом. Абиякий.
Можливо, особливо допитливий учень поцікавиться: а з якого такого дива ми ось так легко і просто відкидаємо однакові підстави зліва і справа і прирівнюємо показники ступенів? інтуїція інтуїцією, але раптом, в якомусь рівнянні і для якоїсь підстави даний підхід виявиться невірним? чи завжди законно викидати однакові підстави? на жаль, для суворої математичної відповіді на це цікаве питання потрібно досить глибоко і серйозно занурюватися в загальну теорію пристрою і поведінки функцій. А трохи конкретніше-в явище суворої монотонності. зокрема, суворої монотонності показової функції y = a x . Оскільки саме показова функція та її властивості лежать в основі розв’язку показових рівнянь, так.) розгорнуту відповідь на це питання буде дано в окремому спецуроці, присвяченому вирішенню складних нестандартних рівнянь з використанням монотонності різних функцій.)
Пояснювати детально цей момент зараз – це лише виносити мозок середньостатистичному школяреві і відлякувати його завчасно сухою і важкою теорією. Я цього робити не буду.) бо наше основне на даний момент завдання-навчитися вирішувати показові рівняння! най-най прості! тому-поки не паримося і сміливо викидаємо однакові підстави. Це можна , повірте мені на слово!) а далі вже вирішуємо еквівалентне рівняння f(x) = g (x). Як правило, більш просте, ніж вихідне показове.
Передбачається, звичайно ж, що вирішувати хоча б , і рівняння, вже без іксів в показниках, народ на даний момент вже вміє.) хто досі не вміє-сміливо закривайте цю сторінку, гуляйте по відповідних ссилочкам і заповнюйте старі прогалини. Інакше несолодко вам доведеться, так…
Я вже мовчу про ірраціональні, тригонометричні та інші звірячі рівняння, які також можуть спливти в процесі ліквідації підстав. Але не лякайтеся, відверту жесть в показниках ступенів ми з вами поки розглядати не будемо: рано ще. Будемо тренуватися лише на найпростіших рівняннях.)
Тепер розглянемо рівняння, які вимагають деяких додаткових зусиль для зведення їх до найпростіших. Для відмінності назвемо їх простими показовими рівняннями . Отже, рухаємося на наступний рівень!
Рівень 1. Прості показові рівняння. Розпізнаємо ступеня! натуральні показники.
Ключовими правилами у вирішенні будь-яких показових рівнянь є правила дій зі ступенями . Без цих знань і умінь нічого не вийде. Та ба. Так що, якщо зіМатематика в школі № 6, 1990 р.с. 37-40.
9. Смирнова модель навчання математики.
Математика в школі №1, 1997 р.с. 32-36.
10. Тарасенко способи організації практичної роботи .
Математика в школі №1, 1993 р.с. 27-28.
11. Про один з видів індивідуальної роботи.
Математика в школі №2, 1994 р.с. 63-64.
12. Хазанкін творчі здібності школярів.
Математика в школі №2, 1989 р.с. 10.
13. Сканаві. Видавець, 1997 р.
14. Алгебра і початку аналізу. Дидактичні матеріали для
15. Кривоногов завдання з математики.
М. «перше вересня», 2002 р.
16. Черкасов. Довідник для старшокласників і
Вступників до вузів. «а з т-прес школа», 2002 р.
17. Жевняк для вступників до вузів.
Мінськ і рф «обозрение», 1996 р.
18. Письмовий д. Готуємося до іспиту з математики. М. Рольф, 1999 р.
19. Вчимося вирішувати рівняння і нерівності.
М. «інтелект-центр», 2003 р.
20. Та ін. Навчально-тренувальні матеріали для підготовки до е г е.
М. «інтелект – центр», 2003 р. І 2004 р.
21 та ін. Центр тестування мо рф, 2002 р., 2003р.
22. Гольдберг рівняння. » квант » №3, 1971 р.
23. Волович м. Як успішно навчати математиці.
Математика, 1997 р. №3.
24 окунев за урок, діти! м. Просвітництво, 1988 р.
25. Якиманська-орієнтоване навчання в школі.
26. Лійметс робота на уроці. М. Знання, 1975 р.
Що таке показове рівняння? приклад.
Отже, показове рівняння … Новий унікальний експонат на нашій загальній виставці найрізноманітніших рівнянь!) як це майже завжди буває, ключовим словом будь-якого нового математичного терміна є відповідний прикметник, який його характеризує. Так і тут. Ключовим словом у терміні «показове рівняння «є слово» показове». Що воно означає? це слово означає, що невідоме (ікс) знаходиться в показниках будь-яких ступенів. І тільки там! це вкрай важливо.
Наприклад, такі прості рівняння:
3 x +1 = 81
5 x + 5 x +2 = 130
4·2 2 x -17 * 2 x +4 = 0
Або навіть такі монстри:
2 sin x = 0,5
Прошу відразу звернути увагу на одну важливу річ: в підставах ступенів (знизу) – тільки числа . А ось в показниках ступенів (зверху) — найрізноманітніші вирази з іксом. Абсолютно будь-які.) все від конкретного рівняння залежить. Якщо, раптом, в рівнянні вилізе ікс де-небудь ще, крім показника (скажімо, 3 x = 18+x 2), то таке рівняння буде вже рівнянням змішаного типу . Такі рівняння не мають чітких правил розв’язку. Тому в даному уроці ми їх розглядати не будемо. На радість учням.) тут ми будемо розглядати тільки показові рівняння в» чистому » вигляді.
Взагалі кажучи, навіть чисті показові рівняння чітко вирішуються далеко не всі і не завжди. Але серед усього багатого різноманіття показових рівнянь є певні типи, які вирішувати можна і потрібно. Ось саме ці типи рівнянь ми з вами і розглянемо. І приклади обов’язково порішаємо.) так що влаштовуємося зручніше і-в дорогу! як і в комп’ютерних «стрілялках», наша подорож буде проходити за рівнями.) від елементарного до простого, від простого – до середнього і від середнього — до складного. По дорозі вас також чекатиме секретний рівень-прийоми і методи вирішення нестандартних прикладів. Ті, про які ви не прочитаєте в більшості шкільних підручників… Ну, а в кінці вас, зрозуміло, чекає фінальний бос у вигляді домашки.)
Рівень 0. Що таке найпростіше показове рівняння? рішення найпростіших показових рівнянь.
Для початку розглянемо якусь відверту елементарщину. З чогось же треба починати, вірно? наприклад, таке рівняння:
2 х = 2 2
Навіть без жодних теорій, за простою логікою і здоровим глуздом ясно, що х = 2. Інакше ж ніяк, вірно? ніяке інше значення ікса не годиться… А тепер звернемо наш погляд на запис рішення цього крутого показового рівняння:
2 х = 2 2
Х = 2
Що ж у нас сталося? а сталося наступне. Ми, фактично, взяли і … Просто викинули однакові підстави (двійки)! зовсім викинули. І, що радує, потрапили в яблучко!
Так, дійсно, якщо в показовому рівнянні зліва і справа стоять однакові числа в яких завгодно ступенях, то ці числа можна відкинути і просто прирівняти показники ступенів. Математика дозволяє.) і далі можна працювати вже окремо з показниками і вирішувати куди більш просте рівняння. Здорово, правда?
Ось і ключова ідея вирішення будь-якого (так-так, саме будь-якого!) показового рівняння: за допомогою тотожних перетворень необхідно домогтися того, щоб зліва і справа в рівнянні стояли однакові числа-підстави в різних ступенях. А далі можна сміливо прибрати однакові підстави і прирівняти показники ступенів. І працювати з більш простим рівнянням.
А тепер запам’ятовуємо залізне правило: прибирати однакові підстави можна тоді і тільки тоді, коли в рівнянні зліва і справа числа-підстави стоять в гордій самоті.
Що значить, в гордій самоті? це означає, без жодних сусідів і коефіцієнтів. Пояснювати.
Наприклад, у рівнянні
3·3 x-5 = 3 2 x +1
Трійки прибирати не можна! чому? тому що зліва у нас стоїть не просто самотня трійка в ступені, а твір 3·3 x-5 . Зайва трійка заважає: коефіцієнт, розумієш.)
Те ж саме можна сказати і про рівняння
5 3 x = 5 2 x +5 x
Тут теж всі підстави однакові – п’ятірка. Але справа у нас не самотня ступінь п’ятірки: там-сума ступенів!
Коротше кажучи, прибирати однакові підстави ми маємо право лише тоді, коли наше показове рівняння виглядає так і тільки так:
a f (x ) = a g (x )
Такий вид показового рівняння називають найпростішим . Або, по-науковому, канонічним . І яке б накручене рівняння перед нами не було, ми його, так чи інакше, будемо зводити саме до такого найпростішого (канонічного) виду. Або, в деяких випадках, до сукупності рівнянь такого виду. Тоді наше найпростіше рівняння можна в загальному вигляді переписати ось так:
F(x) = g(x)
І все. Це буде еквівалентним перетворенням. При цьому в якості f (x) і g(x) можуть стояти абсолютно будь-які вирази з іксом. Абиякий.
Можливо, особливо допитливий учень поцікавиться: а з якого такого дива ми ось так легко і просто відкидаємо однакові підстави зліва і справа і прирівнюємо показники ступенів? інтуїція інтуїцією, але раптом, в якомусь рівнянні і для якоїсь підстави даний підхід виявиться невірним? чи завжди законно викидати однакові підстави? на жаль, для суворої математичної відповіді на це цікаве питання потрібно досить глибоко і серйозно занурюватися в загальну теорію пристрою і поведінки функцій. А трохи конкретніше-в явище суворої монотонності. Зокрема, суворої монотонності показової функції y = a x . Оскільки саме показова функція та її властивості лежать в основі розв’язку показових рівнянь, так.) розгорнуту відповідь на це питання буде дано в окремому спецуроці, присвяченому вирішенню складних нестандартних рівнянь з використанням монотонності різних функцій.)
Пояснювати детально цей момент зараз – це лише виносити мозок середньостатистичному школяреві і відлякувати його завчасно сухою і важкою теорією. Я цього робити не буду.) бо наше основне на даний момент завдання-навчитися вирішувати показові рівняння! най-най прості! тому-поки не паримося і сміливо викидаємо однакові підстави. Це можна , повірте мені на слово!) а далі вже вирішуємо еквівалентне рівняння f(x) = g (x). Як правило, більш просте, ніж вихідне показове.
Передбачається, звичайно ж, що вирішувати хоча б , і рівняння, вже без іксів в показниках, народ на даний момент вже вміє.) хто досі не вміє-сміливо закривайте цю сторінку, гуляйте по відповідних ссилочкам і заповнюйте старі прогалини. Інакше несолодко вам доведеться, так…
Я вже мовчу про ірраціональні, тригонометричні та інші звірячі рівняння, які також можуть спливти в процесі ліквідації підстав. Але не лякайтеся, відверту жесть в показниках ступенів ми з вами поки розглядати не будемо: рано ще. Будемо тренуватися лише на найпростіших рівняннях.)
Тепер розглянемо рівняння, які вимагають деяких додаткових зусиль для зведення їх до найпростіших. Для відмінності назвемо їх простими показовими рівняннями . Отже, рухаємося на наступний рівень!
Рівень 1. Прості показові рівняння. Розпізнаємо ступеня! натуральні показники.
Ключовими правилами у вирішенні будь-яких показових рівнянь є правила дій зі ступенями . Без цих знань і умінь нічого не вийде. Та ба. Так що, якщо зіПрирівнюємо показники:
Залишилося всього лише вирішити це лінійне рівняння. Как? за допомогою тотожних перетворень, вестимо.) дорішайте, чого вже там! множте обидві частини на двійку (щоб прибрати дріб 3/2), переносите складові з іксами вліво, без іксів вправо, приводите подібні – вважайте — і буде вам щастя!
Має все вийти красиво:
X = 4
А тепер знову осмислюємо хід рішення. В даному прикладі нас виручив перехід від квадратного кореня до ступеня з показником 1/2 . Причому тільки таке хитре перетворення нам допомогло скрізь вийти на однакову підставу( двійку), яке і врятувало становище! і, якби не воно, то ми б мали всі шанси назавжди зависнути і так і не впоратися з цим прикладом, так…
Тому не нехтуємо черговим практичним радою:
Якщо в показовому рівнянні присутні коріння, то переходимо від коренів до ступенів з дробовими показниками. Дуже часто тільки таке перетворення і прояснює подальшу ситуацію.
Звичайно ж, негативні та дробові ступені вже набагато складніше натуральних ступенів. Хоча б з точки зору візуального сприйняття і, особливо, розпізнавання справа наліво!
Зрозуміло, що безпосередньо звести, наприклад, двійку в ступінь -3 або ж четвірку в ступінь -3/2 не така вже й велика проблема. Для знаючих.)
А ось піди, наприклад, з ходу зміркуй, що
0,125 = 2 -3
Або
Тут тільки практика і багатий досвід рулять, так. І, звичайно ж, чітке уявлення, що таке негативна і дробова ступінь. а також – практичні поради! так-так, ті самі зелені .) сподіваюся, що вони все-таки допоможуть вам краще орієнтуватися у всьому різношерстому різноманітті ступенів і значно збільшать ваші шанси на успіх! так що не нехтуємо ними. Я не дарма зеленим кольором пишу іноді.)
Зате, якщо ви станете на » ти » навіть з такими екзотичними ступенями, як негативні і дробові, то ваші можливості у вирішенні показових рівнянь колосально розширяться, і вам вже буде по плечу практично будь-який тип показових рівнянь. Ну, якщо не будь-який, то відсотків 80 всіх показових рівнянь — вже точно! так-так, я не жартую!
Отже, наша перша частина знайомства з показовими рівняннями підійшла до свого логічного завершення. І, в якості проміжного тренування, я традиційно пропоную трохи порішати самостійно.)
Завдання 1.
Щоб мої слова про розшифровку негативних і дробових ступенів не пропали даром, пропоную зіграти в невелику гру!
Уявіть у вигляді ступеня двійки числа:
Відповіді (в безладді):
Вийшло? відмінно! тоді робимо бойове завдання-вирішуємо найпростіші і прості показові рівняння!
Завдання 2.
Вирішити рівняння (всі відповіді – в безладді!):
5 2x-8 = 25
2 5x-4-16 x+3 = 0
Відповіді:
X = 16
X 1 = -1; x 2 = 2
X = 5
Вийшло? дійсно, вже куди простіше-то!
Тоді вирішуємо наступну партію:
(2 x +4) x -3 = 0,5 x * 4 x -4
35 1-x = 0,2-x * 7 x
Відповіді:
X 1 = -2; x 2 = 2
X = 0,5
X 1 = 3; x 2 = 5
І ці приклади однієї лівої? відмінно! ви ростете! тоді ось вам на закуску ще примірники:
Відповіді:
X = 6
X = 13/31
X = -0,75
X 1 = 1; x 2 = 8/3
І це вирішено? що ж, респект! знімаю капелюх.) значить, урок пройшов недаремно, і початковий рівень вирішення показових рівнянь можна вважати успішно освоєним. Попереду-наступні рівні і більш складні рівняння! і нові прийоми і підходи. І нестандартні приклади. І нові сюрпризи.) все це-в наступному уроці!
Щось не вийшло? значить, швидше за все, проблеми в . Або в . Або в тому і іншому відразу. Тут вже я безсилий. Можу в черговий раз запропонувати лише одне — не лінуватися і прогулятися по ссилочкам.)
Продовження слід.)